4763. From list of edges to adjacency matrix

The simple not directed graph is given by the list of its edges. Print its representation as an adjacency matrix.

Input. The first line contains two integers n (1 ≤ n ≤ 100) – number of vertices and m (1 ≤ m ≤ n * (n – 1) / 2) – number of edges. Next m lines contain m pairs of integers, each pair gives one edge of the graph.

Output. Print the adjacency matrix of the graph.

Sample input	Sample output
3 3 1 2 2 3 1 3	0 1 1 1 0 1 1 1 0

SOLUTION

graphs

Algorithm analysis

Read the edges, construct the adjacency matrix of undirected graph and print it.

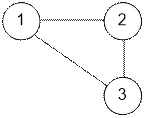
Example

The graph given in the example has the form:

Algorithm realization

Declare the adjacency matrix g.

#define MAX 110

int g[MAX][MAX];

Read the adjacency matrix. For each edge of the graph (a, b) set g[a][b] = g[b][a] = 1.

scanf("%d %d",&n,&m);

memset(g,0,sizeof(g));

for(i = 0; i < m; i++)

{

scanf("%d %d",&a,&b);

g[a][b] = g[b][a] = 1;

}

Print the adjacency matrix of the graph.

for(i = 1; i <= n; i++)

{

for(j = 1; j <= n; j++)

printf("%d ",g[i][j]);

printf("\n");

}

Java realization

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int m = con.nextInt();

int g[][] = new int[n+1][n+1];

for(int i = 0; i < m; i++)

{

int a = con.nextInt();

int b = con.nextInt();

g[a][b] = g[b][a] = 1;

}

for(int i = 1; i <= n; i++)

{

for(int j = 1; j <= n; j++)

System.out.print(g[i][j] + " ");

System.out.println();

}

con.close();

}

}